For most intents and purposes, water is considered to be incompressible.  Realistically, though, water can and will compress a little bit when under immense pressures such as those at the bottom of the ocean.  This brings up an interesting question:  If you bring a sample of high-pressure deep sea water back to the surface enclosed in a container, what happens to the container?

Deep sea oceanographers working with water sample bottles collecting samples from depths of over 6000m get the rare opportunity to observe exactly this question in practice, and the answer is…not much happens.

The bottles go down, take their deep sea samples from depths where the hydrostatic pressure can be as high as 10,000 psi or more, and come back to surface practically the same as if they had been sampling in shallow waters.  No bulging of bottles, no high-pressure jets of water as the researchers drain their samples.  The most that researches may notice is a slight *pop* as they open the drain valves on deep sample bottles vs shallower sample bottles (or, if sample bottles are left full for several hours, sometimes the end caps will pop off with a *BANG* as the enclosed water samples gradually warm up and dissolved gases come out of solution).

But why is this the case?  What happens to all the water pressure?  What forces are actually imposed on the water sample bottles?  Inquiring minds want to know.

When a deep sea water sample is brought to surface, it no longer has kilometers worth of water sitting on top of it to create the high hydrostatic pressure it experienced at depth.  As the sample equalizes its pressure with that of the shallower water outside of the water sample bottle, the sample will expand (slightly).

This is the same thing that happens with the air in a bag of chips taken up in airplane:  The air inside the bag at ground level is at a higher pressure than the air outside the bag at cruising altitude.  The portion of air inside the bag will expand in volume as the plane climbs such that the pressure in the bag matches the lower pressure at altitude.  Although the pressure inside the bag is lower at altitude, the bag is still stretched and under stress.  The actual “pressure” that the bag has to hold up against is driven by how much the air wants to expand to equalize its pressure with the airplane cabin pressure at altitude.

Similarly, the effective pressure felt by a water sample bottle containing a deep sea water sample is not the water’s hydrostatic pressure at depth, but rather the pressure exerted by the water as it attempts to expand to a lower-pressure volume within the water sample bottle.  Calculating the effective “pressure” felt by the water sample bottle must account for both the effects of the water attempting to expand, as well as the “hugging” effects of the water sample bottle material resisting the expansion.

This is very similar to the pressure conditions occurring in press-fits, where a cylinder of one material is forced into a slightly-smaller hub of another material.  In this case, the decompressing water is the “cylinder” and the water sample bottle is the “hub”.  The solid mechanics formulas associated with analyzing press-fits can thus be applied to analytically investigate how much pressure a decompressing deep-sea sample actually imparts on a water sample bottle.

Press fit stress analysis starts with calcuating the radial interference “delta”, defined as the difference in the radius of the nominal hub size and the larger cylinder size.  In the case of water sample bottles, this comes down to calculating what the deep sea sample’s expanded volume would be if it weren’t constrained by a water sample bottle, and (assuming the sample expands isotropically in all directions as it depressurizes) solving for the change in dimensions relative to the original volume.

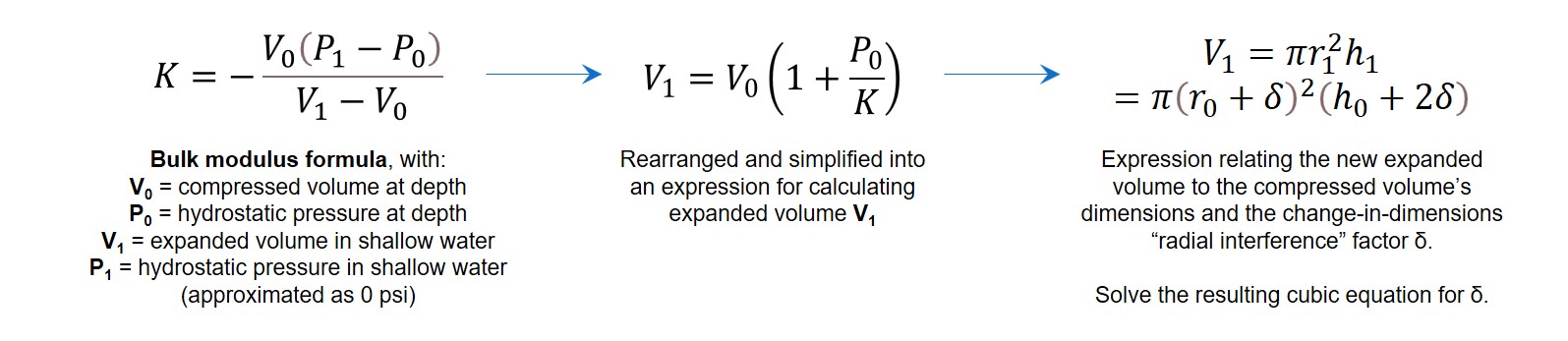
After calculating the radial interference, it can be used in the solid mechanics formula for calculating the interference pressure created by cramming a cylinder of one material into a hub of a different material.  This formula is intended to be applied to metals, though, which have both a Poisson’s ratio and a modulus of elasticity.

While water has a bulk modulus property defining its compressibility, as a liquid it fundamentally cannot support tensile loads and therefore cannot have a modulus of elasticity property.  The interference pressure formula can be rewritten with water’s “modulus of elasticity” in terms of its bulk modulus and Poisson’s ratio instead.  However, the Poisson’s ratio for incompressible liquids (like water) is taken as 0.5, which by inspection will drive the interference pressure to effectively be zero.

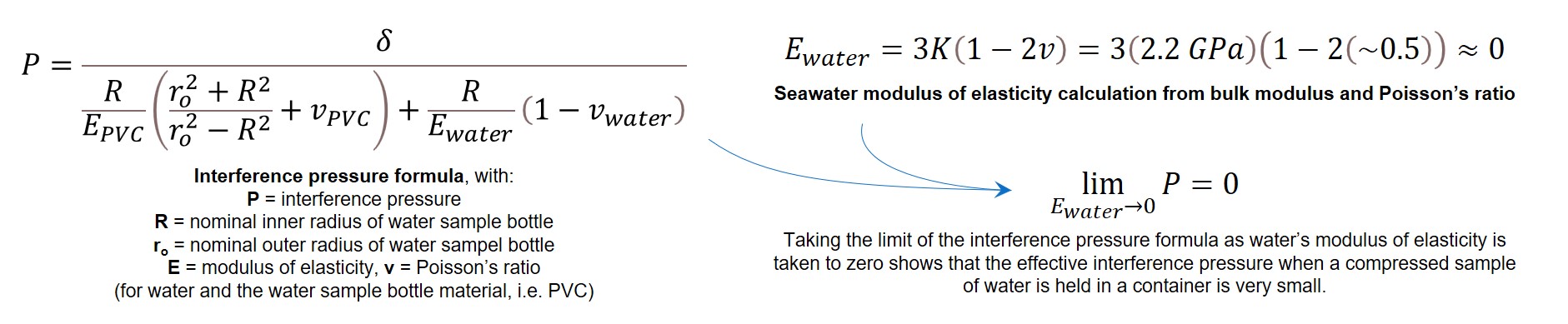
As a check, the interference pressure formula can be evaluated with water’s Poisson’s ratio approximated as 0.4999 (very, very close to 0.5, to attempt to account for its slight compressiblity even if tension-related material properties are otherwise nonsense for a liquid).

For standard sizes of water sample bottles made from Schedule 40 PVC pipe and collecting samples from, say, 7000m depths, the effective interference pressure that the bottles feel in reaction to the deep sea water samples attempting to decrompress upon being brought to surface should only be on the order of ~5 psi or less.  Unlike the hydrostatic pressure at 7000m depth of over 10,000 psi, this is well within PVC’s capabilities to handle – hence, no bursting bottles!

If water samples did maintain their hydrostatic pressure once captured, water sample bottles wouldn’t be able to even sample beyond 1000m depths without rupturing, let alone 7000m depths.  Since this is not the reality, it further reinforces the fact that the hydrostatic pressure at depth is not maintained as the bottles return to surface, and instead the water samples equalize their pressure with that of shallower water as they come up.

As deep sea water sample bottles are brought back to surface, the water samples trapped inside the bottles will attempt to expand to equalize pressure with the lower pressure outside of the bottles at shallower depths.  The effective stresses felt by the water sample bottle are not related to the hydrostatic pressure of the water when it was collected at dept, but rather to the “hugging” forces of the bottle resisting the water’s expansion as it is brought to lower pressure shallower depths.

The bottle is more accurately analyzed using solid mechanics equations traditionally used for analyzing press fits between metal parts, which reveal that effective interference pressures generated in the bottle by the decompressing water are effectively negligible.  This aligns with what oceanographers directly observe during research cruises with deep sea water sampling, where there is no significant difference between the deep sea sample bottles vs the shallow sample bottles.

Solid mechanics theory and formulas for analyzing press fits:  https://www.faculty.fairfield.edu/wdornfeld/ME311/PressCylinderHam.pdf

PVC material properties:  https://ipexna.com/wp-content/uploads/2022/08/submittal-data-us-ipex-xirtec-pvc.pdf

Standard water sample bottle dimensions:  https://technautics.com.au/wp-content/uploads/2023/05/1010-NISKIN-DATA-SHEET.pdf

Sch40 PVC pipe dimensions:  https://www.pvcfittingsonline.com/resource-center/pvc-pipe-dimensions-18-through-24/